Percents and Proportions
Can you tell me what number 63 is 90% of? Don't get scared, FRN, and please don't comment that I ended my question with a preposition. I just want to know the answer, and how you calculated it.
There are several ways that I know how to calculate the answer.
1. In my head. Which is now referred to as mental math. All the times when we were kids, when you didn't show your work and you said to the math teacher, I did it in my head? I never got credit for that. Well now, you can explain yourself by saying, I did mental math. The teacher will look at you, smile, and give you full credit. No matter if you pulled the answer out of your behind.
2. By converting the number sentence. 63 = 90/100 * N. N is what we don't know, and so we can solve for N by multiplying both sides by 100/90, and we get 70. To double check, if we say 63/70, we do indeed find the answer to be 90%.
3. Using a proportion, #1. This is a variation on #2 above. We can say that 63 out of N is equal to 90%, so the proportion would look like this: 63/N = 90/100. This is where I would cross-multiply and say that 63 * 100 = 90 * N, and again, we'd solve for N. Divide both sides by 90 and we have 6300/90 = 70.
4. Using a proportion, # 2. Again, a variation of #2 and #3, really. You can set up the same equation, 63/N = 90/100, but this time, you look and see how you get from 90 to 63. If you're good enough at math, you'd realize that you multiplied 90 by 0.7 to get 63. Since you did that to the numerator, you HAVE to multiply the denominator by the same value. So 100* 0.7 = 70. This sort of business works better for the 6th grade student if it is obvious what you multiplied the numerator by, such as in the following example. 25/N = 50/100.
Now, as if you didn't have enough ways to solve this problem, teachers are throwing another option at you. Instead of picking a short method from above (I really like #3 and use that all the time, like this morning, when I needed to adjust a recipe for pancakes.) my kids are learning about double number lines.
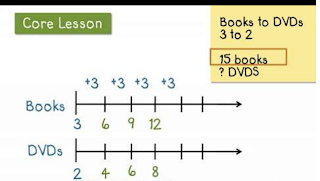
5. Double number lines. You basically have to model the percentage by dividing the number into the number of parts you think you need to divide it into. And then you write 63 at the 90% mark. It was too much to do the math here, but I have a picture of a simpler example. See if you can do it. It's part of the common core, and kids need to know how.
Yeah, it isn't that intuitive, is it, to make this double number line. Mental math is easy here, and really, just setting up the proportion, if your brain fails you, takes no time at all. In my opinion, we're scaring more folks than helping with this method. In fact, they're making mountains out of molehills. I'd already be on question number 5 of my paper if I'd chosen to use a proportion to figure out the answer to 63 is 90% of? Instead, I'm still spinning my wheels, trying to figure out what I need to divide my number into.
So my take on all of this? If the children are understanding the traditional method, why bother changing it? I've used proportions my entire life and they have yet to fail me. I don't need a number line and a piece of paper and 5 minutes to do them, either.
There are several ways that I know how to calculate the answer.
1. In my head. Which is now referred to as mental math. All the times when we were kids, when you didn't show your work and you said to the math teacher, I did it in my head? I never got credit for that. Well now, you can explain yourself by saying, I did mental math. The teacher will look at you, smile, and give you full credit. No matter if you pulled the answer out of your behind.
2. By converting the number sentence. 63 = 90/100 * N. N is what we don't know, and so we can solve for N by multiplying both sides by 100/90, and we get 70. To double check, if we say 63/70, we do indeed find the answer to be 90%.
3. Using a proportion, #1. This is a variation on #2 above. We can say that 63 out of N is equal to 90%, so the proportion would look like this: 63/N = 90/100. This is where I would cross-multiply and say that 63 * 100 = 90 * N, and again, we'd solve for N. Divide both sides by 90 and we have 6300/90 = 70.
4. Using a proportion, # 2. Again, a variation of #2 and #3, really. You can set up the same equation, 63/N = 90/100, but this time, you look and see how you get from 90 to 63. If you're good enough at math, you'd realize that you multiplied 90 by 0.7 to get 63. Since you did that to the numerator, you HAVE to multiply the denominator by the same value. So 100* 0.7 = 70. This sort of business works better for the 6th grade student if it is obvious what you multiplied the numerator by, such as in the following example. 25/N = 50/100.
Now, as if you didn't have enough ways to solve this problem, teachers are throwing another option at you. Instead of picking a short method from above (I really like #3 and use that all the time, like this morning, when I needed to adjust a recipe for pancakes.) my kids are learning about double number lines.
5. Double number lines. You basically have to model the percentage by dividing the number into the number of parts you think you need to divide it into. And then you write 63 at the 90% mark. It was too much to do the math here, but I have a picture of a simpler example. See if you can do it. It's part of the common core, and kids need to know how.
So my take on all of this? If the children are understanding the traditional method, why bother changing it? I've used proportions my entire life and they have yet to fail me. I don't need a number line and a piece of paper and 5 minutes to do them, either.
Comments